Є речі, які спершу здаються складними. Але варто розкласти їх на прості частини — і все стає на свої місця. Так само й з модулем вектора. Поки звучить абстрактно, але якщо уявити звичайний маршрут із точки А в точку Б — одразу стає зрозуміло, про що мова.
Модуль вектора — це просто довжина. А формула, яка її описує, — це ваша особиста мапа до розв’язання завдань у геометрії, фізиці чи програмуванні.
Як виглядає модуль вектора в 2D
Уявіть, що ви стоїте на розі двох вулиць. Один крок вліво, інший — вперед. Ви зробили два кроки, але фактично віддалилися від старту не на два, а трохи менше. І ось модуль вектора допомагає знайти цю реальну відстань.
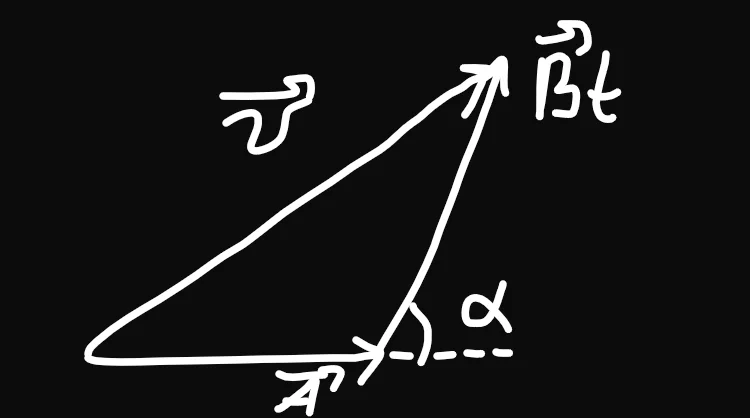Формула виглядає так:
|a| = √(x² + y²)
Наприклад, у вас вектор з координатами (3; 4). Підставляємо:
|a| = √(3² + 4²) = √(9 + 16) = √25 = 5
Ви фактично зрушили на 5 одиниць. Просто, правда? У такій формі модуль вектора формула застосовується навіть у побутових задачах: від вимірювання відстані на карті до роботи з зображенням у Photoshop.
Хочете відчути цей принцип? Візьміть лінійку, проведіть пряму між двома точками. Це і є модуль — без хитрих вигинів.
Що змінюється, якщо додається ще одна координата
Тепер уявіть, що ви не просто йдете по місту, а ще й підіймаєтесь сходами. З’являється третій напрям — вгору. І це вже простір 3D. Тут формула трохи довша:
|a| = √(x² + y² + z²)
Нехай координати вектора (2; 3; 6). Маємо:
|a| = √(2² + 3² + 6²) = √(4 + 9 + 36) = √49 = 7
Так працює обчислення в просторі. Його використовують, наприклад, у 3D-дизайні або при моделюванні руху в фізиці.
Подумайте про квадрокоптер. Щоб розрахувати його шлях, треба врахувати не лише координати по горизонталі, а й висоту. Саме тоді в гру вступає формула модуля вектора в просторі.
Спробуйте самостійно: придумайте координати, уявіть рух — і порахуйте модуль. Це затягує.
Якщо вектор у n-вимірному просторі
Може здатися, що більше вимірів — більше плутанини. Насправді все лишається знайомим. Просто додаються нові координати:
|a| = √(x₁² + x₂² + … + xₙ²)
Принцип той самий: піднесли до квадрата всі координати, додали, витягнули корінь. От і все.
Цю формулу активно використовують у машинному навчанні. Уявіть, що кожна координата — це характеристика об’єкта. І вам треба порахувати, наскільки об’єкти «схожі». Розрахунок модуля допоможе дізнатись це дуже точно.
Не лякайтесь термінів. Просто уявіть, що ви порівнюєте два рецепти пирога. Кожен інгредієнт — це координата. А відстань між рецептами — це модуль вектора між ними.
Як ще можна знайти модуль
Є ситуації, коли замість координат вектора ви маєте дві точки. Наприклад, початок і кінець шляху. У такому випадку спершу обчислюємо координати вектора:
a = (x₂ – x₁; y₂ – y₁; z₂ – z₁)
А потім застосовуємо ту ж знайому формулу. Наприклад:
Точка A: (1; 2), точка B: (4; 6)
Вектор AB = (4−1; 6−2) = (3; 4)
|AB| = √(3² + 4²) = 5
Цей підхід часто використовують в навігації — від GPS до логістики. Ви маєте маршрут і хочете дізнатись, наскільки він дійсно довгий.
Є ще один спосіб — через теорему косинусів, якщо відомі кут і довжина між векторами. Але це вже для тих, хто хоче трохи зануритись глибше. Якщо цікаво — спробуйте знайти приклади самостійно.
Навіщо це все знати в реальному житті
Навіщо це все знати в реальному життіБагато хто думає, що математика — лише для підручників. Але вона буквально живе в наших телефонах, іграх, навігаторах.
Коли ви фотографуєте й редагуєте зображення — програма рахує, наскільки змістити піксель. І це теж модуль вектора.
Коли фізик обчислює силу — це вектор. А його модуль — те, що реально діє на тіло.
Коли інженер моделює міст чи каркас — довжини векторів визначають розтяг чи тиск.
Знання простих речей, як-от модуль вектора, відкриває двері до розуміння складніших процесів. І ви вже не просто дивитесь на формули, а розумієте, як вони працюють.
Кожна формула має свій сенс. Але поки ви не відчуєте її на прикладі, вона лишається просто набором символів. Модуль вектора — це не про суху теорію, а про рух, про напрямок, про довжину шляху, який ми щодня долаємо — у просторі чи в думках.
Якщо ви дочитали до цього місця — спробуйте обчислити модуль свого власного «вектора» за день. Скільки ви пройшли, скільки змінили, на скільки просунулись уперед?
І пам’ятайте: складне — це просто, якщо подивитися з правильного кута.
